

What shapes can you make out of buckyballs?
A polyomino is a shape that consists of unit squares pasted together. This is an extension of the word domino, two squares placed side by side. But the word poly means meny, hence we may have many squares arranged to form a particular shape. Can this piece be used, over and over again, to tile a rectangle? If so, the order of the polyomino is the smallest number of pieces that will tile a rectangle. It is notoriously difficult to determine the order of even modest polyominoes.
Of course the polyomino might already be a rectangle, as illustrated by the domino. Thus it's order is 1 (not very interesting). A triominoe, three squares pasted together, can assume only two distinct shapes. The straight line has order 1 and the L shape has order 2. The 5 distinct tetrominoes have order 1, 1, 2, 4, and 0. The troublesome tetromino, that looks like a set of stairs, has order 0 because it cannot tile a rectangle. As you march along the floor of the rectangle, you must always slide another piece under the notch of the previous piece, and the pattern propagates forever. You can tile the first quadrant, but not a finite rectangle.
If you are familiar with the Hex ™ puzzle, which has been on the market for decades, you already know the 12 pentominoes well. The hex puzzle asks you to tile a 6×10 rectangle with these 12 pieces. This is an interesting problem in itself, and I have written a C program to find all the solutions, as well as the 5×12, 4×15, and 3×20 rectangles. This and all other software referenced by this website can be obtained, followed, or cloned from github. Collaboration is certainly welcome; I can't do this all by myself.
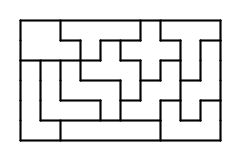
When I was in junior high I built the 35 distinct hexominoes out of lego and tried to fit them into a 14×15 frame. I even thought about marketing the puzzle, since the Hex puzzle (based on the 12 pentominoes) attained commercial success. But try as I might, I could not fit the 35 pieces into the frame. The puzzle wouldn't sell well if there was no solution! Finally I had an epiphany and applied the checkerboard argument. Most pieces cover 3 white squares and 3 black, but an odd number of hexominoes cover 4 white squares and 2 black, or 2 white squares and 4 black. This is a contradiction, hence there is no solution. (Wikipedia hexomino also gives this checkerboard proof.) Of course I could always toss out one of these offending pieces and try to tile a 12×17 rectangle with the remaining 34 pieces, but that is not aesthetically pleasing. I mean, which one do you toss out? The 35 hexominoes can however be packed into a right triangle. This is a stroke of good fortune; 210 is a triangular number, and the triangle covers 110 white squares and 100 black squares. An example solution is shown below. This is original with me.
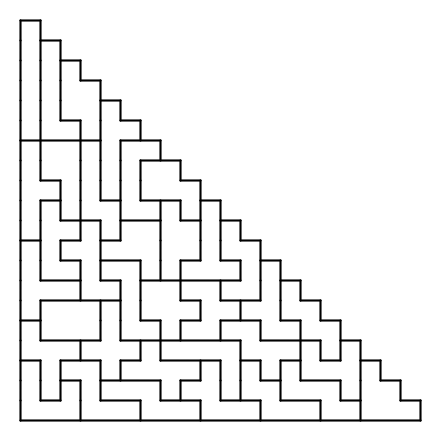
You can pack all ominoes, from the single square up to the 35 hexominoes, into a rectangle that is 13 by 23.
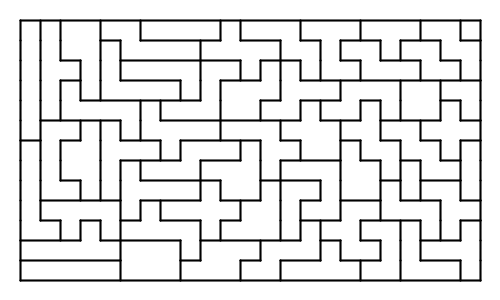
There are 108 heptominoes, one has a hole in it and cannot participate in a solid packing. If you want a rectangle with a hole in the center, allowing for all 108, that's 108*7+1, 757, which is prime, so no dice there. All this is in wikipedia heptomino. However, I found that the 107 simply connected pieces can make a rather long rectangle 107 by 7.

Returning to a single polyomino, most of the pentominoes have order 0 because they have the same tongue-in-groove problem as the stair tetrominoe. The viable pentominoes have order 1 (5 in a row), 2 (L shape), 2 (Utah), and 10 (4 in a row with a square above the second).
Most of the hexominoes are easily solved, i.e. they tile a rectangle with just a few pieces or they don't - except for the Y hexominoe, 5 squares in a row and another above the second. Here we have a simple shape consisting of 6 squares pasted together, yet we must write a computer program to determine whether it tiles a rectangle. I wrote such a program in 1987, and was the first to discover that this shape does indeed tile a rectangle, and its order is 92. (Science News, November 14, 1987.) Using variations of this program, I have discovered many other tilings. I find these patterns quite fascinating. They illustrate the incredible complexity and beauty of mathematics.
Click here for a parade of tiled rectangles. The base polyominoes in these patterns have orders ranging from 2 to 396. These patterns and the software that produced them are copyright © Karl Dahlke, 2001, and cannot be used for commercial purposes (such as puzzles and games) without written consent. Personal use is fine however, such as these beautiful quilts that Donna made for her children and grandchildren.

Are you interested in sets of polyominoes? The general problem is undecidable, yet many interesting questions are within reach. People have explored pairs of pentominoes or hexominoes, asking which pairs can tile a rectangle. For instance, the C and + pentominoes have order 3 (as a set), even though neither can tile a rectangle on its own. My tiling program can analyze a set of polyominoes, provided all shapes in the set have the same number of squares. I am investigating sets of hexominoes, as well as individual polyominoes, whose order is still undetermined.
You may be wondering about higher dimensions. Three dimensional polyominoes are built by pasting unit cubes together. Some can be used to tile rectangular boxes; others cannot. And the same is true in higher dimensions, beyond the boundaries of our imagination. An interesting inconsistency emerges as we move from 2 to 3 dimensions. In 2 dimensions a Flatlander would notice that some of the pieces in the "solution" were reflected through a mirror. He cannot imagine the 3-dimensional being that picked some of the pieces "up" and "flipped them over". He can only assume there were two sets of pieces, some left-handed and some right-handed, and somebody used pieces from either set, as he wished, to tile the rectangle. Indeed, polyomino tilings aren't very interesting if you don't do this. In contrast, we 3-dimensional beings are content with the 24 spatial orientations. It doesn't occur to us to reflect some of the pieces through a mirror, probably because we can't. Indeed, these reflections don't seem to be necessary - there are plenty of interesting patterns without them.
The thre smallest spacial tetrominoes are formed by placing a cube on top of an L triomino. These all have order 2. Interestingly, the stair tetromino, which could not tile a rectangle in the plane, has order 6 in 3 dimensions (Left as an exercise for the reader). The flat pentomino that looks like the letter C also has order 6. The spatial pentomino formed by placing a cube ontop of a 2×2 square has order 4. This is just the edge of a glorious, uncharted wilderness. My tiling software, referenced earlier, would have to be completely restructured to handle 3-dimensional polyominoes.
If you are interested in tilings, or mathematical patterns in general, Brian Wichmann has assembled a large collection, from all branches of mathematics. They are available on a CD-ROM, carefully indexed and thoroughly documented. I was proud to contribute to this work. You can purchase this compilation, The World of Patterns, ISBN 981-02-4619-6, from WorldScientific.com.
You may also be interested in the book, Polyominoes, by Solomon W. Golomb. This is rated 5.0 out of 5 stars.
Golden Visas, Golden Rectangles, and Mathematical Terms of Greece:
Greek Mathematical Terms
|
Golden Rectangles
|
Greece Golden Visa
Send any comments or feedback to me via email. Or visit my home page.